题型一 平行、垂直关系的证明
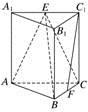
例1 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
(1)求证:平面ABE⊥平面B1BCC1;
(2)求证:C1F∥平面ABE;
(3)求三棱锥E-ABC的体积.
(1)证明 在三棱柱ABC-A1B1C1中,BB1⊥底面ABC.
因为AB⊂平面ABC,
所以BB1⊥AB.
又因为AB⊥BC,BC∩BB1=B,
所以AB⊥平面B1BCC1.
又AB⊂平面ABE,
所以平面ABE⊥平面B1BCC1.
(2)证明 方法一 如图1,取AB中点G,连接EG,FG.
因为E,F分别是A1C1,BC的中点,
所以FG∥AC,且FG=AC.
因为AC∥A1C1,且AC=A1C1,
所以FG∥EC1,且FG=EC1,
所以四边形FGEC1为平行四边形,
所以C1F∥EG.
又因为EG⊂平面ABE,C1F⊄平面ABE,
所以C1F∥平面ABE.
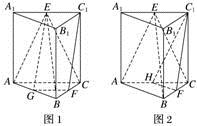
方法二 如图2,取AC的中点H,连接C1H,FH.
因为H,F分别是AC,BC的中点,所以HF∥AB,
又因为E,H分别是A1C1,AC的中点,
所以EC1∥AH,且EC1=AH,
所以四边形EAHC1为平行四边形,
所以C1H∥AE,
又C1H∩HF=H,AE∩AB=A,
所以平面ABE∥平面C1HF,
又C1F⊂平面C1HF,
所以C1F∥平面ABE.
(3)解 因为AA1=AC=2,BC=1,AB⊥BC,
所以AB==.
所以三棱锥E-ABC的体积
V=S△ABC·AA1=×××1×2=.
思维升华 (1)平行问题的转化
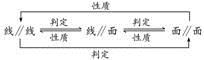
利用线线平行、线面平行、面面平行的相互转化解决平行关系的判定问题时,一般遵循从“低维”到“高维”的转化,即从“线线平行”到“线面平行”,再到“面面平行”;而应用性质定理时,其顺序正好相反.在实际的解题过程中,判定定理和性质定理一般要相互结合,灵活运用.
(2)垂直问题的转化
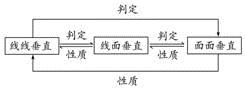
在空间垂直关系中,线面垂直是核心,已知线面垂直,既可为证明线线垂直提供依据,又可为利用判定定理证明面面垂直作好铺垫.应用面面垂直的性质定理时,一般需作辅助线,基本作法是过其中一个平面内一点作交线的垂线,从而把面面垂直问题转化为线面垂直问题,进而可转化为线线垂直问题.
跟踪训练1 如图,在底面是矩形的四棱锥P—ABCD中,PA⊥底面ABCD,点E,F分别是PC,PD的中点,PA=AB=1,BC=2.
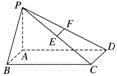
(1)求证:EF∥平面PAB;
(2)求证:平面PAD⊥平面PDC.
证明 (1)以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴,建立如图所示的空间直角坐标系Axyz,则A(0,0,0),B(1,0,0),C(1,2,0),D(0,2,0),P(0,0,1).

∵点E,F分别是PC,PD的中点,
∴E,F,
=,=(1,0,0).
∵=-,
∴∥,
即EF∥AB,
又AB⊂平面PAB,EF⊄平面PAB,
∴EF∥平面PAB.
(2)由(1)可知,
=(0,0,1),=(0,2,0),=(1,0,0),
∵·=(0,0,1)·(1,0,0)=0,
·=(0,2,0)·(1,0,0)=0,
∴⊥,⊥,
即AP⊥DC,AD⊥DC.
又AP∩AD=A,AP,AD⊂平面PAD,
∴DC⊥平面PAD.
∵DC⊂平面PDC,
∴平面PAD⊥平面PDC.

题型二 立体几何中的计算问题
命题点1 求线面角
例2 (2018·浙江)如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.

(1)证明:AB1⊥平面A1B1C1;
(2)求直线AC1与平面ABB1所成的角的正弦值.
方法一 (1)证明 由AB=2,AA1=4,BB1=2,AA1⊥AB,BB1⊥AB,得AB1=A1B1=2,
所以A1B+AB=AA,
故AB1⊥A1B1.
由BC=2,BB1=2,CC1=1,BB1⊥BC,CC1⊥BC,
得B1C1=.
由AB=BC=2,∠ABC=120°,得AC=2.
由CC1⊥AC,得AC1=,
所以AB+B1C=AC,
故AB1⊥B1C1.
又因为A1B1∩B1C1=B1,A1B1,B1C1⊂平面A1B1C1,
所以AB1⊥平面A1B1C1.
(2)解 如图,过点C1作C1D⊥A1B1,交直线A1B1于点D,连接AD.

由AB1⊥平面A1B1C1,
得平面A1B1C1⊥平面ABB1.
由C1D⊥A1B1,平面A1B1C1∩平面ABB1=A1B1,C1D⊂平面A1B1C1,得C1D⊥平面ABB1.
所以∠C1AD即为AC1与平面ABB1所成的角.
由B1C1=,A1B1=2,A1C1=,
得cos∠C1A1B1=,sin∠C1A1B1=,
所以C1D=,
故sin∠C1AD==.
因此直线AC1与平面ABB1所成的角的正弦值是.
方法二 (1)证明 如图,以AC的中点O为原点,分别以射线OB,OC为x,y轴的正半轴,建立空间直角坐标系Oxyz.
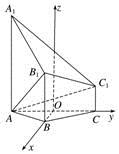
由题意知各点坐标如下:
A(0,-,0),B(1,0,0),A1(0,-,4),B1(1,0,2),C1(0,,1).
因此=(1,,2),=(1,,-2),=(0,2,-3).
由·=0,得AB1⊥A1B1.
由·=0,得AB1⊥A1C1.
又A1B1∩A1C1=A1,A1B1,A1C1⊂平面A1B1C1,
所以AB1⊥平面A1B1C1.
(2)解 设直线AC1与平面ABB1所成的角为θ.
由(1)可知
=(0,2,1),=(1,,0),=(0,0,2).
设平面ABB1的一个法向量为n=(x,y,z).
由得
可取n=(-,1,0).
所以sin θ=|cos〈,n〉|==.
因此直线AC1与平面ABB1所成的角的正弦值是.
思维升华 (1)利用向量求直线与平面所成的角有两个思路:①分别求出斜线和它在平面内的射影直线的方向向量,转化为求两个方向向量的夹角(或其补角);②通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角,取其余角就是斜线和平面所成的角.
(2)若直线l与平面α的夹角为θ,直线l的方向向量l与平面α的法向量n的夹角为β,则θ=-β或θ=β-,故有sin θ=|cos β|=.
跟踪训练2 在直三棱柱ABC-A1B1C1中,△ABC为正三角形,点D在棱BC上,且CD=3BD,点E,F分别为棱AB,BB1的中点.
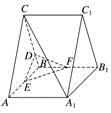
(1)证明:A1C∥平面DEF;
(2)若A1C⊥EF,求直线A1C1与平面DEF所成的角的正弦值.
解 (1)如图,连接AB1,A1B交于点H,
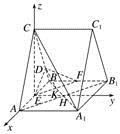
设A1B交EF于点K,连接DK,
因为四边形ABB1A1为矩形,
所以H为线段A1B的中点.
因为点E,F分别为棱AB,BB1的中点,
所以点K为线段BH的中点,
所以A1K=3BK.
又CD=3BD,所以A1C∥DK.
又A1C⊄平面DEF,DK⊂平面DEF,
所以A1C∥平面DEF.
(2)连接CE,EH,由(1)知,EH∥AA1,
因为AA1⊥平面ABC,
所以EH⊥平面ABC.
因为△ABC为正三角形,且点E为棱AB的中点,
所以CE⊥AB.
故以点E为坐标原点,分别以,,的方向为x轴、y轴、z轴的正方向建立如图所示的空间直角坐标系Exyz.
设AB=4,AA1=t(t>0),
则E(0,0,0),A1(2,t,0),A(2,0,0),C(0,0,2),
F,D,
所以=(-2,-t,2),=.
因为A1C⊥EF,所以·=0,
所以(-2)×(-2)-t×+2×0=0,
所以t=2,
所以=(-2,,0),=.
设平面DEF的一个法向量为n=(x,y,z),
则所以
取x=1,则n=(1,,).
又==(-2,0,2),
设直线A1C1与平面DEF所成的角为θ,
则sin θ=|cos〈n,〉|===,
所以直线A1C1与平面DEF所成的角的正弦值为.
命题点2 求二面角
例3 (2018·呼和浩特联考)如图,在四棱锥A-BCDE中,平面BCDE⊥平面ABC,BE⊥EC,BC=2,AB=4,∠ABC=60°.
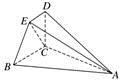
(1)求证:BE⊥平面ACE;
(2)若直线CE与平面ABC所成的角为45°,求二面角E-AB-C的余弦值.
(1)证明 在△ACB中,由余弦定理得cos∠ABC==,
解得AC=2,
所以AC2+BC2=AB2,所以AC⊥BC.
又因为平面BCDE⊥平面ABC,平面BCDE∩平面ABC=BC,AC⊂平面ABC,
所以AC⊥平面BCDE.
又BE⊂平面BCDE,所以AC⊥BE.
又BE⊥EC,AC,CE⊂平面ACE,且AC∩CE=C,
所以BE⊥平面ACE.
(2)解 方法一 因为直线CE与平面ABC所成的角为45°,平面BCDE⊥平面ABC,平面BCDE∩平面ABC=BC,
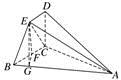
所以∠BCE=45°,所以△EBC为等腰直角三角形.
取BC的中点F,连接EF,过点F作FG⊥AB于点G,连接EG,
则∠EGF为二面角E-AB-C的平面角.
易得EF=BF=1,FG=.
在Rt△EFG中,由勾股定理,得EG==,
所以cos∠EGF==,
所以二面角E-AB-C的余弦值为.
方法二 因为直线CE与平面ABC所成的角为45°,平面BCDE⊥平面ABC,平面BCDE∩平面ABC=BC,
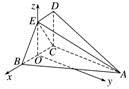
所以∠BCE=45°,所以△EBC为等腰直角三角形.
记BC的中点为O,连接OE,则OE⊥平面ABC,
以O为坐标原点,分别以OB,OE所在直线为x轴、z轴,建立如图所示的空间直角坐标系,
则A(-1,2,0),B(1,0,0),E(0,0,1),
所以=(-2,2,0),=(-1,0,1).
设平面ABE的法向量m=(x,y,z),
则即
令x=,则m=(,1,)为平面ABE的一个法向量.
易知平面ABC的一个法向量为=(0,0,1),
所以cos〈m,〉===,
易知二面角E-AB-C为锐角,
所以二面角E-AB-C的余弦值为.
思维升华 (1)求二面角最常用的方法就是分别求出二面角的两个半平面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角是锐角还是钝角.
(2)利用向量法求二面角的大小的关键是确定平面的法向量,求法向量的方法主要有两种:①求平面的垂线的方向向量;②利用法向量与平面内两个不共线向量的数量积为零,列方程组求解.
跟踪训练3 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,AC∩BD=O,A1O⊥底面ABCD,AB=2,AA1=3.

(1)证明:平面A1CO⊥平面BB1D1D;
(2)若∠BAD=60°,求二面角B-OB1-C的余弦值.
(1)证明 ∵A1O⊥平面ABCD,BD⊂平面ABCD,
∴A1O⊥BD.
∵四边形ABCD是菱形,∴CO⊥BD.
∵A1O∩CO=O,A1O,CO⊂平面A1CO,
∴BD⊥平面A1CO.
∵BD⊂平面BB1D1D,
∴平面A1CO⊥平面BB1D1D.
(2)解 ∵A1O⊥平面ABCD,CO⊥BD,
∴OB,OC,OA1两两垂直,
以O为坐标原点,,,的方向为x,y,z轴的正方向建立如图所示的空间直角坐标系.
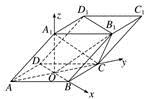
∵AB=2,AA1=3,∠BAD=60°,
∴OB=OD=1,OA=OC=,OA1==.
则O(0,0,0),B(1,0,0),C(0,,0),A(0,-,0),A1(0,0,),
∴=(1,0,0),==(0,,),=+=(1,,).
设平面OBB1的法向量为n=(x,y,z),
则即
令y=,得n=(0,,-1),是平面OBB1的一个法向量.
同理可求得平面OCB1的一个法向量m=(,0,-1),
∴cos〈n,m〉===.
由图可知二面角B-OB1-C是锐二面角,
∴二面角B-OB1-C的余弦值为.
题型三 立体几何中的探索性问题
例4 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2,BC=4,PA=2.

(1)求证:AB⊥PC;
(2)在线段PD上,是否存在一点M,使得二面角M-AC-D的大小为45°,如果存在,求BM与平面MAC所成角的正弦值,如果不存在,请说明理由.
(1)证明 如图,由已知得四边形ABCD是直角梯形,
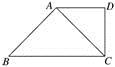
由AD=CD=2,BC=4,可得△ABC是等腰直角三角形,即AB⊥AC,
因为PA⊥平面ABCD,所以PA⊥AB,
又PA∩AC=A,PA,AC⊂平面PAC,
所以AB⊥平面PAC,
所以AB⊥PC.
(2)解 方法一 (几何法)过点M作MN⊥AD交AD于点N,则MN∥PA,
因为PA⊥平面ABCD,所以MN⊥平面ABCD.
过点M作MG⊥AC交AC于点G,连接NG,
则∠MGN是二面角M-AC-D的平面角.
若∠MGN=45°,则NG=MN,
又AN=NG=MN,
所以MN=1,所以MN=PA,MN∥PA,
所以M是PD的中点.
在三棱锥M-ABC中,可得VM-ABC=S△ABC·MN,
设点B到平面MAC的距离是h,
则VB-MAC=S△MAC·h,
所以S△ABC·MN=S△MAC·h,解得h=2.
在Rt△BMN中,可得BM=3.
设BM与平面MAC所成的角为θ,
则sin θ==.
方法二 (向量法)以A为坐标原点,以过点A平行于CD的直线为x轴,AD,AP所在直线分别为y轴、z轴,建立如图所示的空间直角坐标系,
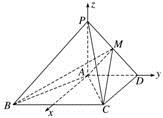
则 A(0,0,0),C(2,2,0),D(0,2,0),
P(0,0,2),B(2,-2,0),=(0,2,-2),=(2,2,0).
易知当点M与P点或D点重合时不满足题意,
设=t(0<t<1),
则点M的坐标为(0,2t,2-2t),
所以=(0,2t,2-2t).
设平面MAC的法向量为n=(x,y,z),则
得
则可取n=.
又m=(0,0,1)是平面ACD的一个法向量,
所以|cos〈m,n〉|==cos 45°=,
解得t=,即点M是线段PD的中点.
此时平面MAC的一个法向量可取n0=(1,-1,),
=(-2,3,1).
设BM与平面MAC所成的角为θ,
则sin θ=|cos〈n0,〉|=.
思维升华 (1)对于线面关系中的存在性问题,首先假设存在,然后在该假设条件下,利用线面关系的相关定理、性质进行推理论证,寻找假设满足的条件,若满足则肯定假设,若得出矛盾的结论则否定假设.
(2)平面图形的翻折问题,关键是搞清翻折前后图形中线面位置关系和度量关系的变化情况.一般地,翻折后还在同一个平面上的性质不发生变化,不在同一个平面上的性质发生变化.
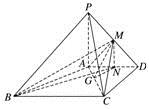
跟踪训练4 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,AB=AC=2,AD=2,PB=,PB⊥AC.
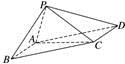
(1)求证:平面PAB⊥平面PAC;
(2)若∠PBA=45°,试判断棱PA上是否存在与点P,A不重合的点E,使得直线CE与平面PBC所成角的正弦值为?若存在,求出的值;若不存在,请说明理由.
(1)证明 因为四边形ABCD是平行四边形,AD=2,
所以BC=AD=2,
又AB=AC=2,
所以AB2+AC2=BC2,所以AC⊥AB,
又PB⊥AC,AB∩PB=B,AB,PB⊂平面PAB,
所以AC⊥平面PAB.
又因为AC⊂平面PAC,
所以平面PAB⊥平面PAC.
(2)解 由(1)知AC⊥AB,AC⊥平面PAB,
分别以AB,AC所在直线为x轴,y轴,
平面PAB内过点A且与直线AB垂直的直线为z轴,建立空间直角坐标系Axyz,
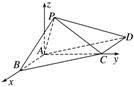
则A(0,0,0),B(2,0,0),C(0,2,0),
=(0,2,0), =(-2,2,0),
由∠PBA=45°,PB=,可得P(1,0,1),
所以=(1,0,1),=(-1,0,1),
假设棱PA上存在点E,
使得直线CE与平面PBC所成角的正弦值为,
设=λ(0<λ<1),
则=λ=(λ,0,λ),=-=(λ,-2,λ),
设平面PBC的法向量n=(x,y,z),
则即
令z=1,可得x=y=1,
所以平面PBC的一个法向量n=(1,1,1),
设直线CE与平面PBC所成的角为θ,则
sin θ= |cos〈n,〉| =
==,
解得λ=或λ=(舍).
所以在棱PA上存在点E,且=,
使得直线CE与平面PBC所成角的正弦值为.

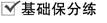
1.在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD.
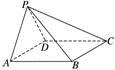
(1)证明:BC⊥PB;
(2)若PA⊥PD,PB=AB,求二面角A-PB-C的余弦值.
(1)证明 取AD中点为E,连接PE,BE,BD,
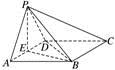
∵PA=PD,∴PE⊥AD,
∵底面ABCD为菱形,
且∠BAD=60°,
∴△ABD为等边三角形,∴BE⊥AD,
∵PE∩BE=E,PE,BE⊂平面PBE,
∴AD⊥平面PBE,
又PB⊂平面PBE,
∴AD⊥PB,
∵AD∥BC,∴BC⊥PB.
(2)解 设AB=2,
∴AD=PB=2,BE=,
∵PA⊥PD,E为AD中点,
∴PE=1,∵PE2+BE2=PB2,
∴PE⊥BE.
以E为坐标原点,分别以EA,EB,EP所在直线为x,y,z轴建立如图所示的空间直角坐标系,

则A(1,0,0),B(0,,0),P(0,0,1),C(-2,,0),
∴=(-1,,0),=(-1,0,1),=(0,-,1),=(-2,0,0).
设平面PAB的法向量为n=(x,y,z),
则即
令y=,则n=(3,,3).
同理可得平面PBC的一个法向量m=(0,,3).
cos〈m,n〉==.
设二面角A-PB-C的平面角为θ,由图易知θ为钝角,
则cos θ=-cos〈m,n〉=-.
∴二面角A-PB-C的余弦值为-.
2.(2019·大连模拟)如图,在三棱柱ABC-A1B1C1中,△ABC和△AA1C均是边长为2的等边三角形,点O为AC中点,平面AA1C1C⊥平面ABC.
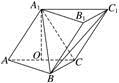
(1)证明:A1O⊥平面ABC;
(2)求直线AB与平面A1BC1所成角的正弦值.
(1)证明 ∵AA1=A1C,且O为AC的中点,
∴A1O⊥AC,
又∵平面AA1C1C⊥平面ABC,平面AA1C1C∩平面ABC=AC,A1O⊂平面AA1C1C,
∴A1O⊥平面ABC.
(2)解 如图,以O为原点,OB,OC,OA1所在直线分别为x轴、y轴、z轴建立空间直角坐标系.

由已知可得O(0,0,0),A(0,-1,0),B(,0,0),A1(0,0,),C1(0,2,),
∴=(,1,0),=(,0,-),=(0,2,0),
设平面A1BC1的法向量为n=(x,y,z),
则即
∴平面A1BC1的一个法向量为n=(1,0,1),
设直线AB与平面A1BC1所成的角为α,
则sin α=|cos〈,n〉|,
又∵cos〈,n〉===,
∴AB与平面A1BC1所成角的正弦值为.
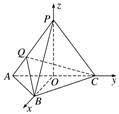
3.(2019·抚顺诊断)如图1,在边长为5的菱形ABCD中,AC=6,现沿对角线AC把△ADC翻折到△APC的位置得到四面体P-ABC,如图2所示.已知PB=4.
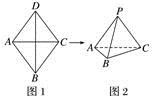
(1)求证:平面PAC⊥平面ABC;
(2)若Q是线段AP上的点,且=,求二面角Q-BC-A的余弦值.
(1)证明 取AC的中点O,连接PO,BO得到△PBO.
∵四边形ABCD是菱形,∴PA=PC,PO⊥AC.
∵DC=5,AC=6,∴OC=3,PO=OB=4,
∵PB=4,∴PO2+OB2=PB2,
∴PO⊥OB.
∵OB∩AC=O,OB,AC⊂平面ABC,∴PO⊥平面ABC.
∵PO⊂平面PAC,∴平面PAC⊥平面ABC.
(2)解 ∵AB=BC,∴BO⊥AC.
易知OB,OC,OP两两垂直.
以O为坐标原点,OB,OC,OP所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系Oxyz.
则B(4,0,0),C(0,3,0),P(0,0,4),A(0,-3,0).
设点Q(x,y,z).
由=,得Q.
∴=(-4,3,0),=.
设n1=(x1,y1,z1)为平面BCQ的法向量.
由得
解得取z1=15,则n1=(3,4,15).
取平面ABC的一个法向量n2=(0,0,1).
∵cos〈n1,n2〉===,
由图可知二面角Q-BC-A为锐角,
∴二面角Q-BC-A的余弦值为.
4.(2019·包头模拟)如图,多面体ABCDEF中,ABCD为正方形,AB=2,AE=3,DE=,二面角E-AD-C的余弦值为,且EF∥BD.
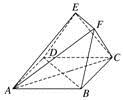
(1)证明:平面ABCD⊥平面EDC;
(2)求平面AEF与平面EDC所成锐二面角的余弦值.
(1)证明 ∵AB=AD=2,AE=3,DE=,
∴AD2+DE2=AE2,
∴AD⊥DE,
又正方形ABCD中,AD⊥DC,且DE∩DC=D,DE,DC⊂平面EDC,
∴AD⊥平面EDC,
又∵AD⊂平面ABCD,
∴平面ABCD⊥平面EDC.
(2)解 由(1)知,∠EDC是二面角E-AD-C的平面角,
作OE⊥CD于O,则OD=DE·cos∠EDC=1,OE=2,
又∵平面ABCD⊥平面EDC,平面ABCD∩平面EDC=CD,OE⊂平面EDC,
∴OE⊥平面ABCD.
取AB中点M,连接OM,则OM⊥CD,
如图,以O为原点,分别以OM,OC,OE所在直线为x轴、y轴、z轴,建立空间直角坐标系,
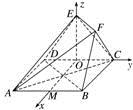
则A(2,-1,0),B(2,1,0),
D(0,-1,0),E(0,0,2),
∴=(-2,1,2),
=(-2,-2,0),
又EF∥BD,知EF的一个方向向量为(2,2,0),
设平面AEF的法向量为n=(x,y,z),
则
取x=-2,得n=(-2,2,-3),
又平面EDC的一个法向量为m=(1,0,0),
∴cos〈n,m〉==-,
设平面AEF与平面EDC所成的锐二面角为θ,
则cos θ=|cos〈n,m〉|=.

5.等边三角形ABC的边长为3,点D,E分别是边AB,AC上的点,且满足==,如图1.将△ADE沿DE折起到△A1DE的位置,使二面角A1—DE—B为直二面角,连接A1B,A1C,如图2.
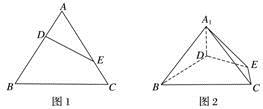
(1)求证:A1D⊥平面BCED;
(2)在线段BC上是否存在点P,使直线PA1与平面A1BD所成的角为60°?若存在,求出PB的长;若不存在,请说明理由.
(1)证明 因为等边三角形ABC的边长为3,
且==,所以AD=1,AE=2.
在△ADE中,∠DAE=60°,由余弦定理得
DE==.
从而AD2+DE2=AE2,所以AD⊥DE.
折起后有A1D⊥DE,因为二面角A1—DE—B是直二面角,
所以平面A1DE⊥平面BCED,
又平面A1DE∩平面BCED=DE,A1D⊥DE,A1D⊂平面A1DE,
所以A1D⊥平面BCED.
(2)解 存在.理由:由(1)可知ED⊥DB,A1D⊥平面BCED.
以D为坐标原点,分别以DB,DE,DA1所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系Dxyz.

设PB=2a(0≤2a≤3),作PH⊥BD于点H,
连接A1H,A1P,
则BH=a,PH=a,DH=2-a.
所以A1(0,0,1),P(2-a,a,0),E(0,,0).
所以=(a-2,-a,1).
因为ED⊥平面A1BD,
所以平面A1BD的一个法向量为=(0,,0).
要使直线PA1与平面A1BD所成的角为60°,
则sin 60°===,
解得a=.此时2a=,满足0≤2a≤3,符合题意.
所以在线段BC上存在点P,使直线PA1与平面A1BD所成的角为60°,此时PB=.

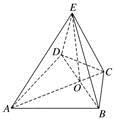
6.如图,在四棱锥E-ABCD中,底面ABCD是圆内接四边形,CB=CD=CE=1,AB=AD=AE=,EC⊥BD.

(1)求证:平面BED⊥平面ABCD;
(2)若点P在侧面ABE内运动,且DP∥平面BEC,求直线DP与平面ABE所成角的正弦值的最大值.
(1)证明 如图,连接AC,交BD于点O,连接EO,
∵AD=AB,CD=CB,AC=AC,
∴△ADC≌△ABC,
易得△ADO≌△ABO,
∴∠AOD=∠AOB=90°,
∴AC⊥BD.
又EC⊥BD,EC∩AC=C,EC,AC⊂平面AEC,
∴BD⊥平面AEC,
又OE⊂平面AEC,∴OE⊥BD.
又底面ABCD是圆内接四边形,
∴∠ADC=∠ABC=90°,
在Rt△ADC中,由AD=,CD=1,
可得AC=2,AO=,
∴∠AEC=90°,==,
易得△AEO∽△ACE,∴∠AOE=∠AEC=90°,
即EO⊥AC.
又AC,BD⊂平面ABCD,AC∩BD=O,
∴EO⊥平面ABCD,
又EO⊂平面BED,∴平面BED⊥平面ABCD.
(2)解 如图,取AE的中点M,AB的中点N,连接MN,ND,DM,

则MN∥BE,
由(1)知,∠DAC=∠BAC=30°,
即∠DAB=60°,
∴△ABD为正三角形,
∴DN⊥AB,
又BC⊥AB,DN,CB⊂平面ABCD,
∴DN∥CB,
又MN∩DN=N,BE∩BC=B,MN,DN⊂平面DMN,BE,BC⊂平面EBC,
∴平面DMN∥平面EBC,
∴点P在线段MN上.
以O为坐标原点,OA,OB,OE所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,
则A,B,E,
M,D,N,
∴=,=,
=,=,
设平面ABE的法向量为n=(x,y,z),
则即
令x=1,则n=(1,,),
设=λ(0≤λ≤1),
可得=+=,
设直线DP与平面ABE所成的角为θ,
则sin θ=|cos〈n,〉|==,
∵0≤λ≤1,∴当λ=0时,sin θ取得最大值.
故直线DP与平面ABE所成角的正弦值的最大值为.